(Click on title slide to access entire slide deck.)

Watch the lecture here.

Lecture 9

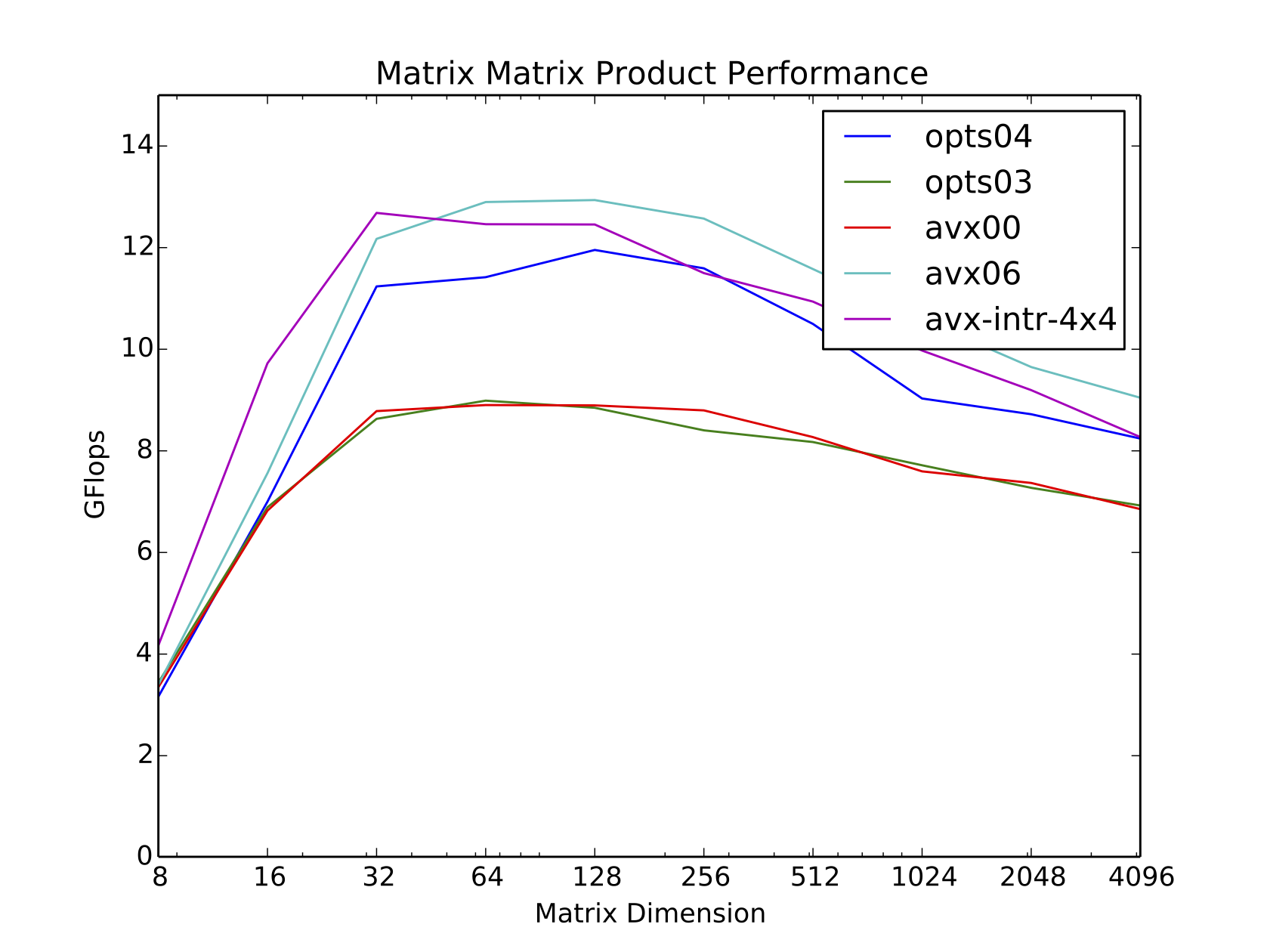
So far we have been looking at how to extract maximum performance (in terms of floating point operations per second) from a CPU. However, in the larger context of scientific computing and problem solving, ultimately what we want to do is compute the answer the in the shortest amount of time.

In this lecture we look at a couple of ways to work smarter (and to work less) in order to reduce time to solution.

We first look at a remarkable algorithm discovered by Volker Strassen (and which now bears his name): Strassen’s algorithm for computing matrix-matrix product with lower than $N^3$ computational complexity.

Next we develop a representation for matrix storage that stores only the information we need for representing a problem and that also results in significant improvements in time to solution.

---